
Nachtrag: Dieser Beitrag ist ein bisschen länglich, wenn Du nur an der Formel interessiert bist, lies‘ lieber den Beitrag ‚Online Kegelrechner‘.
Viele Bastler kommen irgendwann zu dem Punkt, dass sie eine Vorlage für einen abgeschnittenen Kegel benötigen, sei es, um konische Lampenschirmchen aus gemustertem Vellum für Lichterketten, zu machen, sei es für ein Teil eines Clownskostüms für das Kind, eine Vorlage für ein Schmuckstück aus Metall oder aus Fimo oder um eine Papiermachévase herzustellen.
Ich denke, dass die meisten dann eine klare Vorstellung davon haben, wie breit der Kegel oben und unten sein soll und wie hoch.

Ausserdem wissen wir dann, dass die Vorlage für den Kegel so ähnlich wie eine der nebenstehenden aussehen soll.
Aber wie kommt man von der Höhe und den Durchmessern zu der Vorlage, die nachher auch wirklich den gewünschten Kegel ergibt?
Ich stand vor genau so einer Frage und fand dabei math central.
Dort kann man Fragen stellen und sich die Antworten zu bereits gestellten Fragen angucken.
Zum Thema ‚Kegel‘ gibt es bereits mehrere Antworten (einfach in das Suchfeld ‚cone‘ eingeben) und ich habe aus diesen Antworten versucht, eine ganz einfache Anleitung zur Konstruktion von Kegeln zu erstellen.
Beim ersten Lesen scheint es vielleicht kompliziert zu sein, aber wenn man ‚genau nach Kochbuch‘ vorgeht, ist es nicht schwierig. Ein Taschenrechner ist allerdings für die meisten von uns notwendig, denn wir brauchen später die Quadratwurzel eines Wertes.
Zwischendurch habe ich ein bisschen Basiswissen eingestreut, ich musste mir nämlich alles mühsam wieder zusammensuchen, was ich vor Urzeiten einmal gelernt und inzwischen vollkommen vergessen hatte ;-)
Und die eigentlichen Formeln habe ich mit einem  am Anfang markiert.
am Anfang markiert.
Viel Spass damit!
 (Bild zum Vergrößern anklicken)
(Bild zum Vergrößern anklicken)
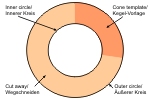
Zunächst einmal: Woraus besteht so eine Kegelvorlage?
Auf dem Bild links sieht man, dass unsere Vorlage aus je einem äußeren und einem inneren Kreis besteht und (hellorange) aus einem Stück, das wir wegschneiden müssen.
Wir werden erst einmal bestimmen, wie groß die Kreise sein sollen und später, wieviel wir wegschneiden.
Dazu ermitteln wir erst einmal Durchmesser der beiden Kreise unserer Kegel-Vorlage.
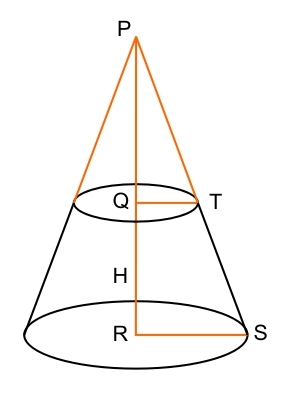
Wenn man sich die Grafik von dem Kegel anguckt (die Grafik habe ich an einer Grafik von math central orientiert), sieht man, dass die beiden Strecken PT und PS der Hälfte der Durchmesser unserer beiden Kreise von oben entsprechen.
(Wenn Du das nicht verstanden hast, ist das nicht schlimm, mach‘ einfach weiter.)
Also werden wir PT und PS errechnen.
Dabei nennen wir die Höhe H, den oberen Durchmesser DiaO und den unteren Durchmesser DiaU.
Für die Formel benötigen wir die gewünschten Radien.
Das ist einfach, denn der Radius ist genau der halbe gewünschte Durchmesser.
Nennen wir also den oberen Radius Ro und den unteren Radius Ru.
Machen wir ein Beispiel: unser Kegel (das ist der vom Foto oben) soll 7cm hoch sein, sein oberer Durchmesser soll 3cm und der untere 7cm betragen.
Achtung: Alle Einheiten müssen immer gleich sein, also nur mm, nur cm oder m ;-)
 H = QR = 7
H = QR = 7
DiaO = 3
DiaU = 7
Da ein Radius genau dem halben Durchmesser entspricht, wissen wir ausserdem:
 Ro = QT = 1,5
Ro = QT = 1,5
 Ru = RS = 3,5
Ru = RS = 3,5
Wir benötigen jetzt noch die Strecken PQ und PR, die wir errechnen müssen (die Formel fand ich in einer Antwort von math central):
 PQ = Ro * H / (Ru – Ro)
PQ = Ro * H / (Ru – Ro)
In unserem Beispiel wäre das PQ = 1,5 * 7 / (3,5 – 1,5) = 5,25
 PR = PQ + H
PR = PQ + H
In unserem Beispiel wäre das PR = 5,25 + 7 = 12,25
Die Formeln für PT und PS lauten:
 PT = sqrt(PQ2 + QT2) = sqrt((PQ * PQ) + (QT * QT))
PT = sqrt(PQ2 + QT2) = sqrt((PQ * PQ) + (QT * QT))
 PS = sqrt(PR2 + RS2) = sqrt((PR * PR) + (RS * RS))
PS = sqrt(PR2 + RS2) = sqrt((PR * PR) + (RS * RS))
Hinweis: ’sqrt‘ heisst ’square root‘ und auf deutsch ‚Wurzel‘ (Symbol: √).
Ich persönlich kann nicht einfach so Wurzelziehen (ausser vielleicht bei 9 ;-))), aber jeder Taschenrechner hat die Funktion und jeder Computer hat (irgendwo!) einen Taschenrechner ;-))
Weiter mit unserem Beispiel:
PT = sqrt((5,25 * 5,25) + (1,5 * 1,5)) = sqrt(27,5625 + 2,25) = sqrt(29,8125) = 5,5
PS = sqrt((12,25 * 12,25) + (3,5 * 3,5)) = sqrt(150,0625 + 12,25) = sqrt(162,3125) = 12,7
Hinweis: Bei unserem Beispiel reicht am Schluss eine Stelle hinter dem Komma vollauf, wobei ich kaufmännisch runde: unter 5 abrunden, über 5 aufrunden.
So, jetzt wissen wir, dass unser äußerer Kreis den Durchmesser von 2 * PS = 25,4 und unser innerer Kreis den Durchmesser von 2 * PT = 11 hat.
Wir haben die ganze Zeit in cm gerechnet, d.h., wir haben 25,4cm und 11cm.
Jetzt können wir uns darum kümmern, herauszufinden, wieviel wir von dem Ring wegschneiden sollen.
Zum Glück brauchen wir da nicht groß zu denken, denn es gibt eine fertige Formel dafür (die ich auch bei mathcentral gefunden habe):
Den Winkel a, der den Bereich kennzeichnet, den wir nicht(!) benötigen, ermitteln wir folgendermassen:
 a = 360 * (1 – ((2 * π * Ru) / (2 * π * PS)))
a = 360 * (1 – ((2 * π * Ru) / (2 * π * PS)))
Hinweis: π heisst ‚Pi‘ und ich verwende 3,14, obwohl die Zahl noch ewig weitergeht.
Für Genauigkeitsfanatiker ;-): das sind die ersten 100 Nachkommastellen von Pi: 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679… ;-)
Rechnen wir weiter mit unserem Beispiel.
Der Winkel a bestimmt sich also folgendermaßen:
a = 360 * (1 – ((2 * π * 3,5) / (2 * π * 12,7))) = 360 * (1 – (21,991 / 79,796)
= 360 * (1 – 0,276) = 360 * 0,724 = 260,64 entspricht etwa 261°
 (Bild zum Vergrößern anklicken)
(Bild zum Vergrößern anklicken)
Super!
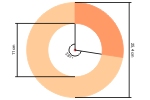
Und was machen wir jetzt mit der ermittelten Gradzahl?
Wir schneiden sie weg ;-)
 (Bild zum Vergrößern anklicken)
(Bild zum Vergrößern anklicken)
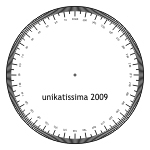
Wer kein Geodreieck hat, kann die Gradscheibe ausdrucken und ausschneiden.
Die Scheibe dann genau mittig in den Ring legen und mit dem Lineal Linien von der Mitte zur 0/360° Markierung und (in unserem Fall) von der Mitte bis zur 261° Markierung ziehen.
Die Linien sehen dann so aus wie die gestrichelten Linien auf dem vorigen Bild und markieren den Bereich, den wir wegschneiden müssen.
 Hinweis: Ich empfehle, die Kegel-Vorlage erst mit Zeitungs- o.ä. Papier zu machen.
Hinweis: Ich empfehle, die Kegel-Vorlage erst mit Zeitungs- o.ä. Papier zu machen.
Um die Mitte zu finden, kann man dann die ungeschnittenen Kreise einfach 2x in der Hälfte falten (s. Foto). Dann ist es einfach, die Gradscheibe präzise zu plazieren.
Links:
Bei math central (englisch, französisch, spanisch):
 Liste bereits beantworteter Fragen
Liste bereits beantworteter Fragen
 Frageformular
Frageformular
 Suchformular
Suchformular
 Antwort auf Frage mit dem Betreff: ‚Constructing a cone‘
Antwort auf Frage mit dem Betreff: ‚Constructing a cone‘
 Antwort auf Frage mit dem Betreff: ‚Pattern for a truncated cone‘
Antwort auf Frage mit dem Betreff: ‚Pattern for a truncated cone‘
Bei Wikipedia (deutsch): Die ersten 100 Nachkommastellen von Pi
Bei Wikipedia (englisch): Die ersten 50 Nachkommastellen von Pi
Hier bei unikatissima:
 Beiträge mit dem Stichwort ‚Fimo‘
Beiträge mit dem Stichwort ‚Fimo‘
 Beiträge mit dem Stichwort ‚Papiermaché‘
Beiträge mit dem Stichwort ‚Papiermaché‘









 am Anfang markiert.
am Anfang markiert.



 Hinweis: Ich empfehle, die Kegel-Vorlage erst mit Zeitungs- o.ä. Papier zu machen.
Hinweis: Ich empfehle, die Kegel-Vorlage erst mit Zeitungs- o.ä. Papier zu machen.

